I believe, and have said in earlier posts here and here on this blog, that the Equivalence Relation Theorem is the modern pons asinorum, the bridge which you must cross in order to become a mathematician: it is essential to be able to think about an object whose elements are equivalence classes of an equivalence relation on another object (for example, cosets of an ideal in a ring are the elements of the quotient ring).
This morning, I nearly found my own head on a pole on this bridge.
With Celia Glass and Robert Schumacher, I am looking at acyclic orientations of graphs. There is a simple formula for the number of acyclic orientations of the graph obtained from a complete graph on n vertices by deleting r pairwise disjoint edges:
.
On first inspection, this is a straightforward inclusion-exclusion formula, and should have a straightforward proof. Maybe it does, but I was unable to find one.
Any acyclic orientation of a graph G arises from a total order of the vertices, or in other words (if the vertex set is {1,…,n}) a permutation of this set. Call two permutations equivalent if they give the same acyclic orientation of G. Our job is to count equivalence classes of this relation.
Now inclusion-exclusion works fine for subsets but not so well for equivalence relations. I spent a bit of time trying to get Möbius inversion on the partition lattice to work, without success. Eventually I found a proof. First, you figure out that the size of the equivalence class containing a permutation is 2k, where k is the number of “missing edges” mapped to consecutive positions by the permutation. Then we proceed as follows. Write down a formula for the number of permutations in which some given “missing edges” are mapped to consecutive positions. Then use inclusion-exclusion to count the permutations for which these and no more are mapped to consecutive positions. Divide by 2k to get the number of equivalence classes into which these permutations fall. Sum over all subsets of the missing edges to get the total number of equivalence classes. Then a chain of formal manipulations:
- reverse the order of summation;
- gather up terms where the set of missing edges has a given size;
- notice that the Binomial Theorem can be applied;
- now gather up terms where the set in the outer summation has a given size.
The final line gives the required formula.
This description may not be clear enough for you to reconstruct. But am I missing something simple?

Can’t you just count the number of total orders on the vertices with the property that non-adjacent vertices are not order-adjacent? This seems to me to give the formula by inclusion-exclusion (with the j-th term in the sum counting the number of total orders in which exactly j pairs of non-adjacent vertices are order-adjacent).
Oh… except that I’d need to take some powers of 2 into account. So perhaps the j-th term should instead count partial orders in which exactly j pairs of non-adjacent vertices are incomparable (and everything else comparable).
Nice pike, er, pic …
I’m afraid that my posts above are rather incoherent. Sorry! Here’s a better argument.
Let {(a_i,b_i) : i = 1,..,r} be the pairs of non-adjacent vertices of G; we consider these as ordered pairs (which is equivalent to choosing an orientation of the complement of G). Now let us look at the number N of labellings of G with the numbers 1,..,n, such that for each such pair (a_i,b_i), the label attached to a_i is never greater by exactly 1 than the label attached to b_i. Then N is the number of acyclic orientations. (Each such labelling specifies a total order, and only one order from each equivalence class is picked out.)
Now let J be a subset of {1,..,r}, and let X_J be the set of labellings of the vertices such that the label of a_i is greater by 1 than the label of b_i for all i in J. Then |X_J| = (n-j)! where j=|J|. Now inclusion-exclusion gives your formula.
Indeed, as I was walking home with a packet of exam scripts to mark, I came up with exactly your argument. Great minds think alike! But I think that the equivalence relation formulation will be essential for various extensions that I have in mind.
With respect to the total orders. For each equivalence class of permutations there should also be a corresponding set of DAGs — those whose transitive closure is the reflexive reduction of the partial order. A disjoint pair of vertices is eliminated if it can be transitively closed.
This follows from the relation

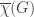 is the number of acyclic orientations,
is the number of acyclic orientations, 
 , and
, and  and
and 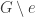
 . This is (iii’)
. This is (iii’)
where
is an edge of
are got by deleting and contracting the edge
in Theorem 1.2 of Richard Stanley’s classic paper on acyclic
orientations.