In part 2 of this series, I explained that it was inspired by a conversation with John Conway in Fine Hall, Princeton, in 1996. I’d like to finish off with the second part of that conversation. I understand that some of this is due to Clark Kimberling, and I don’t know how to apportion the credit. But there are some mysteries here.
Recall from part 3 that the ratio of successive Fibonacci numbers tends to the golden ratio α = (1+√5)/2.
Now let us suppose that a growing plant produces leaves, each one a fraction (α−1) of a circle further round the stem than the one before. (This is the phenomenon of phyllotaxis, and various explanations, more or less convincing, have been given for it; I will take it as a given.) We can mark the positions of successive leaves on a circle, with angles (in multiples of 2π) measured from the position of the starting leaf, number 0. So leaf number n appears at angle {nα}, where the curly brackets { } denote the fractional part.
When leaf number n appears, the circle is already divided into n intervals by the preceding leaves; suppose that there are an intervals between the zeroth leaf and the nth, and bn intervals between the nth leaf and the zeroth. Thus, an+bn = n+1.
What can be said about the ordered pairs (an,bn)?
The answer relies on the theory of continued fractions, which I discussed in part 4. The ratios of successive Fibonacci numbers are good rational approximations to α, in a precise sense which implies that the differences between Fnα and Fn+1 alternate in sign but decrease in magnitude as n increases. So, if n = Fk+1, then (an,bn) is equal to (1,n) if k is odd, and is (n,1) if k is even.
So, if we follow the sequence of Fibonacci numbers, then the number 1 bounces from side to side of the ordered pair.
Moreover, the approximation property implies that the only time when an or bn is equal to 1 is when n is a Fibonacci number.
What about other values? The following table gives the first few:
| n | an | bn |
| 1 | 1 | 1 |
| 2 | 1 | 2 |
| 3 | 3 | 1 |
| 4 | 2 | 3 |
| 5 | 1 | 5 |
| 6 | 5 | 2 |
| 7 | 3 | 5 |
| 8 | 8 | 1 |
| 9 | 5 | 5 |
| 10 | 2 | 9 |
| 11 | 9 | 3 |
| 12 | 5 | 8 |
| 13 | 1 | 13 |
| 14 | 10 | 5 |
| 15 | 5 | 11 |
| 16 | 15 | 2 |
| 17 | 9 | 9 |
| 18 | 3 | 16 |
| 19 | 15 | 15 |
| 20 | 8 | 13 |
| 21 | 21 | 1 |
| 22 | 13 | 10 |
| 23 | 5 | 19 |
| 24 | 20 | 5 |
| 25 | 11 | 15 |
You might like to spend a few minutes spotting patterns in this table before reading on.
In part 2, I explained how the natural numbers can be partitioned into Fibonacci-like sequences indexed by the non-negative integers: the first entry in each sequence is the smallest number which has not previously occurred; the second is obtained from it by applying the “Fibonacci successor function”, and the remaining entries by the usual Fibonacci recurrence. The second row of the table begins 4, 7, 11, 18, …. Now look at the corresponding entries of the table: (2,3), (3,5), (9,3), (3,16), …. This time, it is the number 3 which “bounces” from side to side as we proceed. In the third sequence, 6, 10, 16, …, the number 2 bounces. The table below gives the “bouncing number” t for the nth sequence.
| n | t |
| 0 | 1 |
| 1 | 3 |
| 2 | 2 |
| 3 | 5 |
| 4 | 8 |
| 5 | 5 |
| 6 | 9 |
| 7 | 5 |
| 8 | 10 |
| 9 | 15 |
| 10 | 9 |
I don’t know what the pattern here is. In 1996, I think, Conway didn’t know either. I am not sure if more is known now. If so, and anyone would like to tell me about it, or write it up, I would be delighted!

Pingback: On Fibonacci numbers and the golden ratio « Maximal determinant blog
Pingback: Weekly links for March 25 | God plays dice
Apologies for replying to a 3-year-old posting!
The most natural unit interval to consider for this is not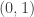 , but rather
, but rather 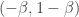 , where
, where 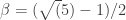 . If the budding function takes values in this interval, then the Fibonacci successor function is given simply by multiplication by $\latex -\beta$. Some of the phyllotactic properties you mention are quite easy to understand in this setting, such as the existence of the “bouncing numbers”. (The “bouncing” occurs because
. If the budding function takes values in this interval, then the Fibonacci successor function is given simply by multiplication by $\latex -\beta$. Some of the phyllotactic properties you mention are quite easy to understand in this setting, such as the existence of the “bouncing numbers”. (The “bouncing” occurs because 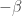 is negative.)
is negative.)
There is a simple approximation for these numbers which appears to be very good. For the row of the successor table with leading entry k, the bouncing number is just the position of the -th bud at the time when it emerges, counting from
-th bud at the time when it emerges, counting from  into the negative part of the unit interval. Since the budding function
into the negative part of the unit interval. Since the budding function  distributes buds very uniformly through the interval, we would expect the number of buds lying between the
distributes buds very uniformly through the interval, we would expect the number of buds lying between the  -th bud and
-th bud and  to be approximately
to be approximately 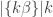 . This approximation is correct to within a margin of
. This approximation is correct to within a margin of 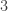 for the first 100000 bouncing numbers (which is as far as I have checked). For instance, the bouncing number in the 100000th row is 121917, and the approximation is 121915.248… .
for the first 100000 bouncing numbers (which is as far as I have checked). For instance, the bouncing number in the 100000th row is 121917, and the approximation is 121915.248… .
Incidentally, it’s fun to extend the idea of a Fibonacci representation to an arbitrary element of the unit interval, by allowing infinite Fibonacci sets (still with the property that their elements differ by at least 2). Every element of the interval has a unique representation, except for elements where
where  is a negative integer; these each have two representations. (This derives from the fact that the sequence
is a negative integer; these each have two representations. (This derives from the fact that the sequence 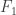 ,
,  ,
, 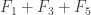 , … and the sequence
, … and the sequence  ,
,  ,
,  , give sequences of buds which converge to opposite ends of the unit interval, and hence to the same point
, give sequences of buds which converge to opposite ends of the unit interval, and hence to the same point  on the stem.)
on the stem.)
No need to apologise for such nice stuff! Thanks John. (I edited your comment to “compile” the LaTeX — this involves writing latex immediately after the first dollar sign (and I think you need a space between that and the start of the LaTeX code)).