News reached me today of the death of S. S. Shrikhande, at the age of 102.
I have written about him before; in particular, here, I discussed two things for which he was perhaps best known, which can bear repeating.
One of these is his role, with Bose and Parker, as one of the trio of Euler spoilers who showed that a pair of orthogonal Latin squares (i.e. a Graeco-Latin square) exists for all orders except 2 and 6, disproving a conjecture of Euler (who thought that such a thing would not exist for orders congruent to 2 modulo 4).
The other is a lovely characterisation of a class of strongly regular graphs. The n×n grid graph (with two vertices joined if they lie in the same row or column of a square array) is regular, has the property that two adjacent vertices have n−2 common neighbours, while two non-adjacent vertices have 2 common vertices. Shrikhande showed that there is just one further graph with this property; it is now known as the Shrikhande graph.
The link arises because the 4×4 grid graph and the Shrikhande graph have the properties that their complements are Latin square graphs: the vertices are again the points of the n×n array, filled with the letters of a Latin square, so that two vertices are joined if they lie in the same orw or column or contain the same letter. There are just two different Latin squares of order 4, the Cayley tables of the Klein group and the cyclic group; the first gives the grid graph of order 4, the second the Shrikhande graph.
We know now that the Shrikhande graph is not an unexpected accident, but is related to the existence of the exceptional root system of type E8.

Thanks for this post.
Where do I look at for learning more about the connection with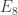 ?
?
You could start with the lecture notes on this blog (Part 3 of the St Andrews Advanced Combinatorics lectures), or the various posts on the ADE affair. Or, in hard copy, my book “Designs, Graphs, Codes and their Links” with Jack van Lint, LMS Student Texts 22.