I have just posted to the arXiv a preprint of a paper with Josephine Kusuma about the subject in the title of this post. (Josephine is on the left in the picture, with Taoyang Wu; the water behind is Windermere.)

Given a set S of words of length n over an alphabet A, we can imagine that the words are stacked in an N×n array, where N is the number of words. We say that S is an orthogonal array of strength t if, given any t columns of the array, each word of length t over A occurs the same number of times in the chosen positions. The strength of S is the largest t for which this holds.
One of Delsarte’s old results is that, if A is a finite field and S a linear code over A, then the strength of S is one less than the minimum Hamming weight of the dual of S. (The dual of S is the set of words having inner product 0 with every word in S; and the Hamming weight of a word is the number of non-zero coordinates.)
Our first theorem is that the same holds if A is a finite commutative ring with identity, and S a linear code over A (meaning a submodule of the free A-module An).
Not so surprising, you might say; but the real surprise is the difficulty of the proof. It depends on a property of finite rings which I didn’t know before this work. (I will from now on say “ring” to mean “commutative ring with identity”.) This is the property:
If I is a proper ideal of A, then the annihilator of I is non-zero.
The proof of this requires a structure theorem for finite rings which I couldn’t find written down anywhere: a finite ring is a direct sum of finite local rings. This is a special case of a general result about completions of semi-local rings (rings with only finitely many maximal ideals), using the observation that any finite ring is semi-local, and a finite ring is its own completion.
The rest of the proof of the extension of Delsarte’s theorem is a fairly easy induction based on this.
The bulk of the paper considers the case of the ring A = Z4, the integers mod 4. This is important because of the work of Hammons, Kumar, Calderbank, Solé and Sloane in the 1990s, which “explained” why certain pairs of non-linear binary codes (the Preparata and Kerdock codes) are related by the MacWilliams transform, a result which holds between a linear code and its dual.
The key is the Gray map, a bijection between Z4 and (Z2)2. The Lee metric on Z4 is the number of “steps round the circle” between two elements: thus, the Lee distance from 1 to 3 is 2, while the Lee distance from 0 to 3 is 1. Now the Gray map is an isometry between Z4 with the Lee metric, and (Z2)2 with the Hamming metric, given by
0 → 00, 1 → 01, 2 → 11, 3 → 10.
As with the Gray map in general, each step around the “circle” of Z4 changes the Gray map image in a single coordinate. (It is this property which makes the Gray map useful in analog-to-digital conversion.)
Thus the image of a linear Z4-code is a possibly non-linear binary code but one whose Hamming weight (and distance) distribution is the same as for the linear Z4-code with which we began.
Now we conjecture the following analogue of Delsarte for this situation:
The strength of the Gray map image of a linear Z4-code S is one less than the Lee weight of the dual of S.
We cannot prove this conjecture, but it holds in many examples, and we can at least prove an inequality one way round. Moreover, the conjecture holds for codes whose duals are generated by a single element.

The fact that a finite (commutative unital) ring is a direct sum
of finite local rings is a special case of the theorem that
any Artinian ring is a finite direct product of Artinian local rings.
This is a a standard theorem: it is Theorem 8.7 in Atiyah and
Macdonald’s Introduction to Commutative Algebra.
Thanks, that is easier.
My challenge (which is maybe a bit silly) is: is there a completely elementary proof of the fact that any proper ideal in a finite commutative unital ring has non-zero annihilator? It looks like something that should be completely obvious …
If is a proper ideal of the finite ring
is a proper ideal of the finite ring  then
then 
 . By Nakayama’s Lemma, there is some
. By Nakayama’s Lemma, there is some 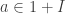
 with
with  nonzero
nonzero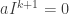 and so
and so  has a nonzero annihilator.
has a nonzero annihilator.
for some
with $\latex aI^n=0$. Thus there is a
but